抽象化を哲学する vol. 2
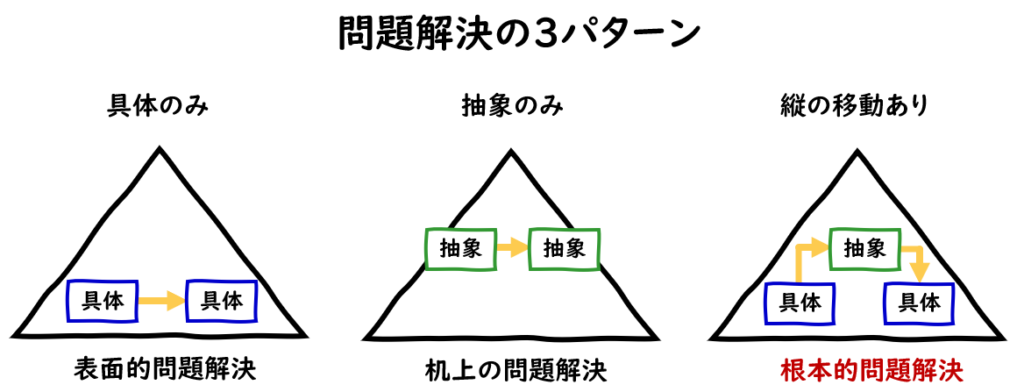
前回、『具体 ⇒ 抽象 ⇒ 具体』という『縦』の移動を行うことが、質の良いアウトプットを出すために重要という話をしました。
でも、縦に移動しろと言われてもどうやってやればいいんですか?って方のために、『具体 ⇒ 抽象 ⇒ 具体』の縦移動を行うための考え方[1]を紹介したいと思います。
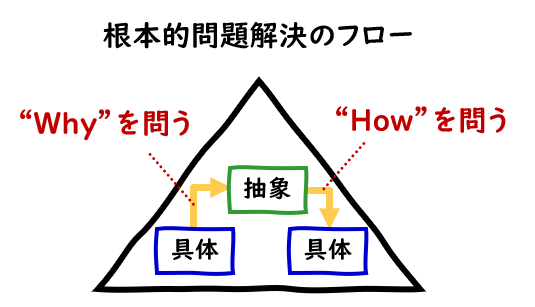
具体 ⇒ 抽象(抽象化)=『Why』を問う
まずは『具体 ⇒ 抽象』の抽象化フェーズです。抽象化するには『Why(なぜ)』を問います。
例えば、あなたが新製品開発プロジェクトのメンバーで、上司から、ステッピングモータ1軸・ボールねじ・直動ガイドを組み合わせたようなあるユニットの詳細設計を任されたとします。
ここで、上司から与えられた構成を何の疑いもなくそのまま採用し、設計してしまうのは三流の設計者のやることだと思います。
優秀な設計者は必ず設計時に『具体 ⇒ 抽象』(抽象化)を行います。
<第一段階の抽象化>
・なぜボールねじを使うのか?その他の直動変換ではダメか?
・なぜステッピングモータを使うのか?その他のアクチュエータではダメか?
などです。
そして上記を考えてくと、その過程で必ずこの設計に求められている要求仕様にスポットが当たります。
<第二段階の抽象化>
・なぜこのようなスペックを求められているのか?(スピードや精度)
・なぜこのようなスペースの制約があるか?
実は絶対的な制約と思われていたことも、ある条件下では制約でなくなったりする場合もあります。そういった部分も紐解いていかないと、製品全体として良いものは作れません。
そのためには、上司だけでなく、他の設計者や営業などの他部署との関わりも出てくるため、主体的な姿勢が必要になります。
すなわち、部分最適でなく全体最適を目指した相互コミュニケーションが必要になります。
上記を考えていくと、さらに上位の視点まで視野が広がります。
<第三段階の抽象化>
・なぜこのユニットが必要なのか?
・そもそも使用するお客様は何を求めているか?
このように、なぜを問い続けることで抽象化が進み、より上位の視点で自分の仕事を捉えることができます。
このような姿勢は、トヨタの「なぜなぜ5回」や、ホンダの「A00」と本質的には同じであり、抽象化がとても重要なことであることを物語っています。
上記は製品開発の例ですが、他の例も下記に示します。
<製品企画段階の例>
お客様の「顕在ニーズ」から「潜在ニーズ」を探るフェーズがまさに抽象化が必要なフェーズだと思います。
お客様の生の声にただ従ってしまうと、本当に良い製品のコンセプトは作れません。なぜお客様はそう言っているのか。Whyを問いましょう。
<流用設計の例>
過去の設計者がなぜそのように設計したのか。Whyを問いましょう。Whyを問うことで設計意図が見えてきます。過去の設計者(生み出した世代)の人たちの意図を汲み取っていかないと、何も根本的に変えられない小手先の変化しか生み出せない設計者になってしまいます。
抽象 ⇒ 具体(具体化)=『How』を問う
Whyを突き詰めて問題を抽象化できたら、次にその解決策を考えるために具体化を行います。具体化には『How(どのように)』を問います。
抽象化する前とした後では、Howの選択肢(自由度)がとても広がっていることが分かると思います。景色が広がるため、本当に良い手段も見つけられる可能性が高まります。具体から具体は見えにくいのですが、抽象から具体は見やすいのです。地上からは隣町の様子は見えませんが、空からは見ることができます。
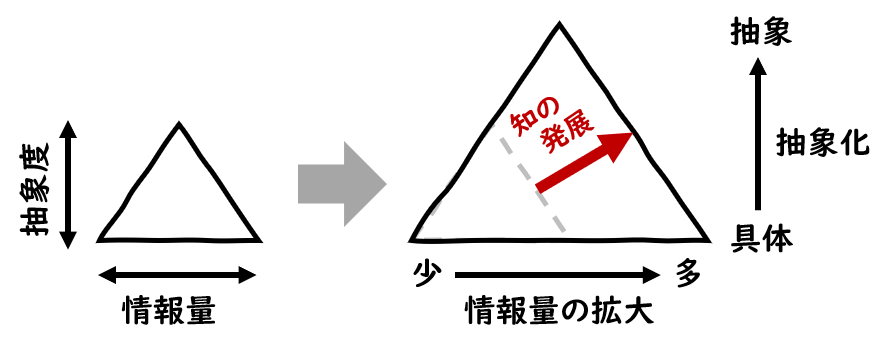
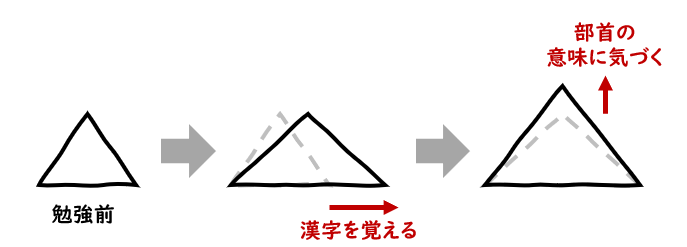
具体化には、ピラミッドの横軸(知識の幅)が必要になります。知識の幅が狭いと、せっかく広い景色が見えたにもかかわらず、良い解にたどり着けません。
新製品開発の場合であれば、プロジェクトメンバーで抽象的な視点を共有したうえで、メンバーで議論することがとても重要だと思います。ここで担当者が自分の知識の幅でしか物事を考えられないと、製品としての可能性を狭めることになってしまいます。
自分なりによく考えたつもりでも、他のメンバーから意見をもらい「痛いところを突かれた」と思うことはよくあるかと思います。その瞬間は製品開発において大きなターニングポイントだと思います。その時の初動が、後に大きな差を生む場合もあります。
意地をはらず、真摯に他のメンバーの意見を受け入れ、自分なりに解釈し、最終的には自分なりに新たな答えを見つけることで、本当に良い開発ができるのだと思います。
<参考文献>
[1] 「具体 ⇔ 抽象」トレーニング、細谷功 著、PHP研究所