慣性モーメントを分かりやすく説明してみた
「慣性モーメント(イナーシャ)」とは
<抽象度★★★★★>
物体の「回りにくさ」「止まりにくさ」を表す値です。
<抽象度★★★★☆>
直動系の超有名な方程式(ニュートンの運動の法則)
$$ F=ma =m \ddot x$$
[N] = [kg] [m/s2]
を回転系に直すと
$$ \tau =Ja= J \ddot \theta $$
[Nm] = [kg・m2] [rad/s2]
となり、ここに出てくる「J」が「慣性モーメント[kg・m2]」です。
すなわち、回転系における「重さ」を示す値と言えます。
<抽象度★★★☆☆>
機械設計において、慣性モーメントはモータの容量を計算する際に必要になります。
台形の速度プロファイルで回転体の位置決めをする場合、「各加速度」に「慣性モーメント」をかけると、モータに必要なトルクが分かります。(摩擦などの負荷トルクは無視しています)
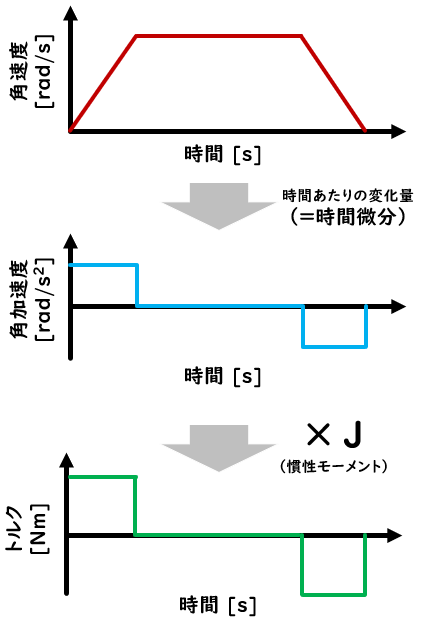
慣性モーメントが大きいと必要なトルクが大きくなり、慣性モーメントが小さいと必要なトルクが小さくなることが分かります。
<抽象度★★☆☆☆>
下図のような質点mの回転を考えます。
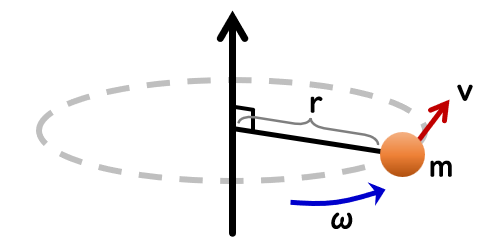
この時、中心軸周りの回転の慣性モーメントは、
$$ J = m r^2 $$
で表されます。
