バイラテラル制御

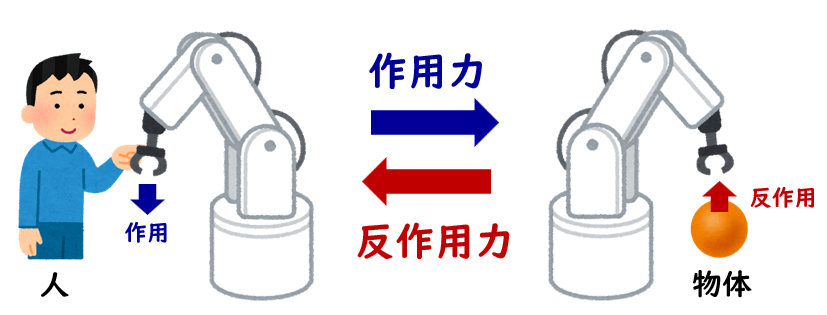
バイラテラル制御^[1] とは、ひと言で言うと「モータを使って触覚を伝送する技術」です。

人が与える作用力と、物体から返ってる反作用力をそれぞれモータ（またはセンサ）で測定できるようにしておきます。

その上で、測定した作用力を物体側へ、反作用力を人側へ送り、各モータで出力します。

ざっくり言うと、このようにして触覚をモータ間で伝達する事ができます。

（厳密にはモード空間での制御が必要ですが、ここでは簡単にイメージのみ説明します。）

バイラテラル制御の面白いところは、触覚情報が、文字通り「情報」になっているため、簡単に加工する事ができるところです。

〈遠隔操作〉

触覚情報を遠隔地に伝送すれば、遠隔操作が可能になります。

〈スケーリング〉

人の力を増幅すれば、テコの原理を扱うように、大きな力で物体を操作する事ができます。

逆に、人の力を減少させて伝えれば、微細で繊細な物体を安全に取り扱うことができます。

〈保存・再現〉

人の与えた作用力をデータとして保存しておけば、CDに音楽を保存して再生するかのように、人間の動作を再現できます。

このように、バイラテラル制御を用いれば、モータを利用したアプリケーションの幅が広がります。

[1] W. Iida and K. Ohnishi, “Reproducibility and operationality in bilateral teleoperation,” The 8th IEEE International Workshop on Advanced Motion Control, 2004. AMC ’04., 2004, pp. 217-222, doi: 10.1109/AMC.2004.1297669.

https://ieeexplore.ieee.org/document/1297669

抽象化を哲学する vol. 2

前回、『具体 ⇒ 抽象 ⇒ 具体』という『縦』の移動を行うことが、質の良いアウトプットを出すために重要という話をしました。
でも、縦に移動しろと言われてもどうやってやればいいんですか？って方のために、『具体 ⇒ 抽象 ⇒ 具体』の縦移動を行うための考え方^[1]を紹介したいと思います。

具体 ⇒ 抽象（抽象化）＝『Why』を問う

まずは『具体 ⇒ 抽象』の抽象化フェーズです。抽象化するには『Why（なぜ）』を問います。

例えば、あなたが新製品開発プロジェクトのメンバーで、上司から、ステッピングモータ１軸・ボールねじ・直動ガイドを組み合わせたようなあるユニットの詳細設計を任されたとします。
ここで、上司から与えられた構成を何の疑いもなくそのまま採用し、設計してしまうのは三流の設計者のやることだと思います。
優秀な設計者は必ず設計時に『具体 ⇒ 抽象』（抽象化）を行います。
＜第一段階の抽象化＞
・なぜボールねじを使うのか？その他の直動変換ではダメか？
・なぜステッピングモータを使うのか？その他のアクチュエータではダメか？
などです。

そして上記を考えてくと、その過程で必ずこの設計に求められている要求仕様にスポットが当たります。
＜第二段階の抽象化＞
・なぜこのようなスペックを求められているのか？（スピードや精度）
・なぜこのようなスペースの制約があるか？
実は絶対的な制約と思われていたことも、ある条件下では制約でなくなったりする場合もあります。そういった部分も紐解いていかないと、製品全体として良いものは作れません。
そのためには、上司だけでなく、他の設計者や営業などの他部署との関わりも出てくるため、主体的な姿勢が必要になります。
すなわち、部分最適でなく全体最適を目指した相互コミュニケーションが必要になります。

上記を考えていくと、さらに上位の視点まで視野が広がります。
＜第三段階の抽象化＞
・なぜこのユニットが必要なのか？
・そもそも使用するお客様は何を求めているか？

このように、なぜを問い続けることで抽象化が進み、より上位の視点で自分の仕事を捉えることができます。
このような姿勢は、トヨタの「なぜなぜ５回」や、ホンダの「A00」と本質的には同じであり、抽象化がとても重要なことであることを物語っています。


上記は製品開発の例ですが、他の例も下記に示します。

＜製品企画段階の例＞
お客様の「顕在ニーズ」から「潜在ニーズ」を探るフェーズがまさに抽象化が必要なフェーズだと思います。
お客様の生の声にただ従ってしまうと、本当に良い製品のコンセプトは作れません。なぜお客様はそう言っているのか。Whyを問いましょう。

＜流用設計の例＞
過去の設計者がなぜそのように設計したのか。Whyを問いましょう。Whyを問うことで設計意図が見えてきます。過去の設計者（生み出した世代）の人たちの意図を汲み取っていかないと、何も根本的に変えられない小手先の変化しか生み出せない設計者になってしまいます。

抽象 ⇒ 具体（具体化）＝『How』を問う

Whyを突き詰めて問題を抽象化できたら、次にその解決策を考えるために具体化を行います。具体化には『How（どのように）』を問います。
抽象化する前とした後では、Howの選択肢（自由度）がとても広がっていることが分かると思います。景色が広がるため、本当に良い手段も見つけられる可能性が高まります。具体から具体は見えにくいのですが、抽象から具体は見やすいのです。地上からは隣町の様子は見えませんが、空からは見ることができます。
具体化には、ピラミッドの横軸（知識の幅）が必要になります。知識の幅が狭いと、せっかく広い景色が見えたにもかかわらず、良い解にたどり着けません。
新製品開発の場合であれば、プロジェクトメンバーで抽象的な視点を共有したうえで、メンバーで議論することがとても重要だと思います。ここで担当者が自分の知識の幅でしか物事を考えられないと、製品としての可能性を狭めることになってしまいます。
自分なりによく考えたつもりでも、他のメンバーから意見をもらい「痛いところを突かれた」と思うことはよくあるかと思います。その瞬間は製品開発において大きなターニングポイントだと思います。その時の初動が、後に大きな差を生む場合もあります。
意地をはらず、真摯に他のメンバーの意見を受け入れ、自分なりに解釈し、最終的には自分なりに新たな答えを見つけることで、本当に良い開発ができるのだと思います。

＜参考文献＞

[1] 「具体 ⇔ 抽象」トレーニング、細谷功 著、PHP研究所

抽象化を哲学する vol. 1

そもそも抽象化とは？

上の図は、知の発展を表現した図です^[1]。
「横軸」の拡大は、知識の「量的」な拡大を意味しています。
「縦軸」は「抽象度」を示しています。上に行くほど「抽象的」、下に行くほど「具体的」な情報であることを意味しています。
例えば、小学生が漢字を勉強する場合、覚えた漢字の数だけ情報量が増えるため、三角形が横軸に広がります。ですが、ただひたすらに覚えるだけでは三角形は横にしか広がりません。
ここで、「さんずい」は水に関係するものであるなど、漢字にはある法則があることに気が付くと、情報を抽象化でき、三角形が縦方向に広がります。

このように、抽象化とは「情報と情報の関係性」に着目し、その共通項・法則を発見することであり、縦方向に三角形を広げることで、具体の世界を俯瞰して眺めることのできる「鳥の目」を得ることができます。縦方向に成長できると、具体の世界の見通しが格段に良くなり、発想が豊かになります。みなさんにもそのような実感をした経験があるのではないでしょうか。

ここでは、抽象化とは何なのかを哲学していきたいと思います。
（哲学≒抽象化であるので、抽象化を抽象化していくということかもしれません。）

大事なのは縦の移動

ここで問題解決の３パターン^[1]を見てみます

左の図は、具体病の人の問題解決です。
実際に起きていることに目が行き、そこに対する断片的な処置を施します。

真ん中の図は、抽象病の人の問題解決です。
机上で考えているだけで具体的な行動に落とし込めません。

右の図が、問題解決のあるべき姿です。
縦の移動を行うことで、起きた事象から根本原因に立ち返って対処できます。

新しい製品の開発を考えてみると・・・
・具体病（左）：過去の設計資産に基づいて、ちょっと変更した設計を行う。（チェンジニアリング）
・抽象病（中）：コンセプトだけ出して、具体的な設計に落とし込めない。（机上の空論）
・縦移動（右）：顕在化した課題から潜在的な課題を導き、根本対策を施した設計をする。（イノベーション）

といったように、縦の移動を行うことで、良い製品の開発を行うことができます。

このように、具体的・抽象的であること自体ではなく、具体 ⇒ 抽象 ⇒ 具体の移動を行うことが重要で、質の良いアウトプットを出すために必要なのです。

＜参考文献＞

[1] 「具体 ⇔ 抽象」トレーニング、細谷功 著、PHP研究所

クロソイド曲線

ここでは、クロソイド曲線の紹介をします。

クロソイド曲線は「曲率の変化」が一定な曲線のことです。
曲率 (curvature) とは、曲線の曲がり具合を示す値であり、曲率を一定にしたまま線を伸ばしていくと円になります。その円の半径を「曲率半径」といい、曲率の逆数になります。

円の曲線の長さ\(q\)と接線ベクトルの角度\(\phi\)の関係を式に表すと以下になります。
$$ \phi=\phi_0+c_1 q $$
\(\phi_0\)は接線ベクトルの角度の初期値です。
ここで曲率\(c_v\)は、\(\phi\)を\(q\)で微分した値であり、円の場合は、
$$ c_v=c_1 = const. $$
となることが分かります。

曲率を曲線の長さに対して一定に変化させていったものがクロソイドで、その曲線の長さ\(q\)と接線ベクトルの角度\(\phi\)の関係は下記になります。
$$ \phi=\phi_0+c_1 q + c_2 q^2$$

円の場合と同様に、\(\phi\)を\(q\)で微分すると、
$$ c_v=c_1 + \frac{1}{2}c_2 q$$
となり、曲線の長さに対して一定の割合で変化していることが分かります。


ここで、わかりやすい例として、車で考えてみたいと思います。
曲線を車の通った道だとすると、曲率はハンドルの傾き（回した量）と同じになります。
ハンドルを一定の傾きで固定した状態で走れば、車の通る道は円を描きます。

車が走った距離に応じて、ハンドルを一定の速度で回していったときに車の通った道が描く曲線がクロソイドになります。

ハンドルを急に切る必要がないため、高速道路の出入り口の曲線の設計などに用いられているそうです。

クロソイド曲線に関して、詳しくはこちらの論文に記載しています。

I. Takeuchi and S. Katsura, “Interpolation of a Clothoid Curve Based on Iterative True-Value Prediction Considering the Discretization Error,” in IEEE Transactions on Industrial Informatics, vol. 14, no. 11, pp. 5156-5166, Nov. 2018, doi: 10.1109/TII.2018.2797925.

https://ieeexplore.ieee.org/document/8269384